1505. Пересечение
отрезков - 2
На
декартовой плоскости задано n
отрезков координатами своих концов. Определить, пересекаются ли они. Множество
отрезков пересекается, если среди них существует хотя бы два, которые имеют как
минимум одну общую точку.
Вход. Каждая
строка содержит целочисленные координаты концов отрезка (x1, y1)
- (x2, y2). Известно, что n ≤ 6*105 и -1000
≤ x1, y1, x2, y2
≤ 1000.
Выход. Вывести
"intersect", если отрезки пересекаются и
"NOT intersect" иначе.
Пример входа
1 1 6 36 1 9 32 5 7 32 3 4 37 2 10 1
Пример выхода
Intersect
РЕШЕНИЕ
геометрия – заметающая прямая
Анализ алгоритма
Повернем все отрезки на малый
угол чтобы ни один из них не был вертикальным. После считывания отрезка
поменяем местами его концы если x2 < x1. Таким образом
координаты
обрабатываемых отрезков удовлетворяют соотношению x1 < x2. Создадим массив точек – концов
отрезков, где с каждой точкой свяжем пару (номер отрезка которому принадлежит
точка, тип конца отрезка – начало или конец). Отсортируем точки по возрастанию
абсцисс.
Далее используем метод заметающей
прямой. Двигаясь слева направо, будем обрабатывать концы отрезков. Отрезки,
которые пересекает текущая заметающая прямая, будем хранить в мультимножестве s. Изначально оно пусто. Текущую абсциссу заметающей прямой храним в глобальной
действительной переменной xcur. Реализуем функцию сравнения двух отрезков a и
b,
пересекающих прямую x = xcur. Для этого
следует вычислить их y координаты пересечения с прямой x = xcur и сравнить между собой. Теперь вставка отрезка в мультимножество s будет
выполняться за логарифмическое время.
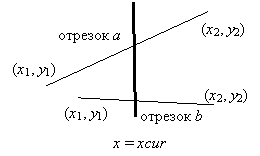
Пусть отрезок а пересекается с прямой x = xcur в точке (xcur, ya). Тогда имеет
место пропорция:
![]()
Откуда
ya = ![]()
Аналогично находится ордината
точки пересечения отрезка b с прямой x
= xcur.
События заметающей прямой
обрабатываются следующим образом:
1. Если текущая точка – начало
отрезка, то втавляем отрезок в мультимножество s и проверяем его на пересечение с соседними по ординате (верхним и нижним)
отрезками, находящимися в s.
2. Если текущая точка – конец
отрезка, то удаляем отрезок из s, а
отрезки, находившиеся выше и ниже его, проверяем на пересечение.
Реализация алгоритма
Объявим глобальную переменную xcur, которая
будет содержать текущую абсциссу заметающей прямой. Объявим классы точки Point
и отрезка Segment.
double xcur;
class Point
{
public:
double x1,
y1;
Point(double
x1 = 0, double y1 = 0)
{
this->x1
= x1; this->y1 = y1;
}
};
class Segment
{
public:
double x1,
y1, x2, y2;
Segment(double
x1 = 0, double y1 = 0, double
x2 = 0, double y2 = 0)
{
this->x1
= x1; this->y1 = y1;
this->x2
= x2; this->y2 = y2;
}
};
Функция
сравнения двух отрезков a и b, пересекающих заметающую прямую x = xcur.
int operator<
(Segment a, Segment b)
{
double y1,
y2;
y1 = a.y1 + (xcur - a.x1) * (a.y2 - a.y1) /
(a.x2 - a.x1);
y2 = b.y1 + (xcur - b.x1) * (b.y2 - b.y1) /
(b.x2 - b.x1);
return y1
< y2;
}
Функция Intersect проверяет, пересекаются ли
отрезки a и b.
int Intersect(Segment a, Segment b);
Мультимножество
s содержит отрезки, пересекающие заметающую прямую x = xcur. Объявим
также несколько итераторов.
multiset<Segment>
s;
multiset<Segment>::iterator
iter, iPrev, iNext;
Входные отрезки храним в векторе v. Множество концов отрезков с дополнительной информацией (номер
отрезка которому принадлежит точка и тип точки – начало (0) или конец (1)
отрезка) храним в
векторе p.
vector<Segment>
v;
vector<pair<Point,pair<int,int> > >
p;
Функция
сортировки точек по неубыванию абсцисс.
int f(pair<Point,pair<int,int> > a,
pair<Point,pair<int,int> > b)
{
if
(a.first.x1 == b.first.x1) return
a.second.second < b.second.second;
return
a.first.x1 < b.first.x1;
}
Основная
часть программы. Читаем входные отрезки и совершаем их обработку перед запуском
заметающей прямой.
n = 0;
while(scanf("%lf
%lf %lf %lf",&x_1,&y_1,&x_2,&y_2) == 4)
{
Поворачиваем отрезок на угол EPS = 0.001 чтобы он не был вертикальным.
x11 = x_1 * cos(EPS) - y_1*sin(EPS);
y11 = x_1 * sin(EPS) + y_1*cos(EPS);
x22 = x_2 * cos(EPS) - y_2*sin(EPS);
y22 = x_2 * sin(EPS) + y_2*cos(EPS);
Первый конец каждого отрезка должен находиться не правее
второго.
if (x22 <
x11) swap(x11,x22), swap(y11,y22);
v.push_back(Segment(x11,y11,x22,y22));
p.push_back(make_pair(Point(x11,y11),make_pair(n,0)));
p.push_back(make_pair(Point(x22,y22),make_pair(n,1)));
n++;
}
Сортируем концы отрезков по неубыванию абсцисс.
sort(p.begin(),p.end(),f);
Запускаем заметающую прямую. Она идет по абсциссам точек,
хранящимся в массиве p.
flag = 0;
for(i = 0; i < p.size(); i++)
{
Если текущая точка – начало отрезка, то вставляем этот
отрезок в мультимножество s и
проверяем, пересекается ли он с верхним и нижним отрезками в мультимножестве.
if
(p[i].second.second == 0)
{
xcur = p[i].first.x1 + 0.1;
iter = s.insert(v[p[i].second.first]);
iPrev = iNext = iter;
if (iPrev
!= s.begin())
{
iPrev--;
if
(Intersect((*iter),(*iPrev))) flag = 1;
}
iNext++;
if (iNext
!= s.end())
{
if
(Intersect((*iter),(*iNext))) flag = 1;
}
} else
{
Если текущая точка – конец отрезка, то устанавливаем
итератор iter на него.
Проверям, пересекаются ли отрезки, находящиеся выше и ниже его. После чего
удаляем из мультимножества s отрезок,
конец которого обрабатываем.
iter = s.find(v[p[i].second.first]);
iPrev = iNext = iter; iNext++;
if
((iPrev != s.begin()) && (iNext != s.end()))
{
iPrev--;
if
(Intersect((*iPrev),(*iNext))) flag = 1;
}
s.erase(iter);
}
if (flag) break;
}
Выводим результат в зависимости от значения переменной flag.
if (!flag)
printf("NOT ");
printf("intersect\n");